Module_1: Complexity Analysis_1
- Apurba Paul
- Jan 12, 2020
- 8 min read
Time and Space Complexity
The complexity of an algorithm is a function describing the efficiency of the algorithm in terms of the amount of data the algorithm must process. There are two main complexity measures of the efficiency of an algorithm:
1. Time complexity is a function describing the amount of time an algorithm takes in terms of the amount of input to the algorithm. In layman’s terms, we can say time complexity is the sum of the number of times each statement gets executed.
2. Space complexity is a function describing the amount of memory (space) an algorithm takes in terms of the amount of input to the algorithm. When we say “this algorithm takes constant extra space,” because the amount of extra memory needed doesn’t vary with the number of items processed.
For any defined problem, there can be N number of solutions. This is true in general. If I have a problem and I discuss the problem with all of my friends, they will all suggest different solutions. And I am the one who has to decide which solution is the best based on the circumstances.
Similarly, for any problem which must be solved using a program, there can be an infinite number of solutions. Let's take a simple example to understand this. Below we have two different algorithms to find the square of a number(for some time, forget that square of any number n is n*n):
One solution to this problem can be, running a loop for n times, starting with the number n and adding n to it, every time.
/*
we have to calculate the square of n
*/
for i=1 to n
do n = n + n
// when the loop ends n will hold its square
return n
Or, we can simply use a mathematical operator * to find the square.
/*
we have to calculate the square of n
*/
return n*n
In the above two simple algorithms, you saw how a single problem can have many solutions. While the first solution required a loop that will execute for n number of times, the second solution used a mathematical operator * to return the result in one line. So which one is the better approach, of course, the second one.
Time Complexity is most commonly estimated by counting the number of elementary steps performed by an algorithm to finish execution. Like in the example above, for the first code the loop will run n number of times, so the time complexity will be n at least and as the value of n will increase the time taken will also increase. While for the second code, the time complexity is constant, because it will never be dependent on the value of n, it will always give the result in 1 step.
And since the algorithm's performance may vary with different types of input data, hence for an algorithm we usually use the worst-case Time complexity of an algorithm because that is the maximum time taken for any input size.
Calculating Time Complexity
Now lets tap onto the next big topic related to Time complexity, which is How to Calculate Time Complexity. It becomes very confusing some times, but we will try to explain it in the simplest way.
Now the most common metric for calculating time complexity is Big O notation. This removes all constant factors so that the running time can be estimated in relation to N, as N approaches infinity. In general you can think of it like this :
statement;
Above we have a single statement. Its Time Complexity will be Constant. The running time of the statement will not change in relation to N.
for(i=0; i < N; i++)
{
statement;
}
The time complexity for the above algorithm will be Linear. The running time of the loop is directly proportional to N. When N doubles, so do the running time.
for(i=0; i < N; i++)
{
for(j=0; j < N;j++)
{
statement;
}
}
This time, the time complexity for the above code will be Quadratic. The running time of the two loops is proportional to the square of N. When N doubles, the running time increases by N * N.
while(low <= high)
{
mid = (low + high) / 2;
if (target < list[mid])
high = mid - 1;
else if (target > list[mid])
low = mid + 1;
else break;
}
This is an algorithm to break a set of numbers into halves, to search a particular field(we will study this in detail later). Now, this algorithm will have a Logarithmic Time Complexity. The running time of the algorithm is proportional to the number of times N can be divided by 2(N is high-low here). This is because the algorithm divides the working area in half with each iteration.
void quicksort(int list[], int left, int right)
{
int pivot = partition(list, left, right);
quicksort(list, left, pivot - 1);
quicksort(list, pivot + 1, right);
}
Taking the previous algorithm forward, above we have a small logic of Quick Sort(we will study this in detail later). Now in Quick Sort, we divide the list into halves every time, but we repeat the iteration N times(where N is the size of the list). Hence time complexity will be N*log( N ). The running time consists of N loops (iterative or recursive) that are logarithmic, thus the algorithm is a combination of linear and logarithmic.
NOTE: In general, doing something with every item in one dimension is linear, doing something with every item in two dimensions is quadratic, and dividing the working area in half is logarithmic.
Types of Notations for Time Complexity
Now we will discuss and understand the various notations used for Time Complexity.
Big Oh denotes "fewer than or the same as" <expression> iterations.
Big Omega denotes "more than or the same as" <expression> iterations.
Big Theta denotes "the same as" <expression> iterations.
Little Oh denotes "fewer than" <expression> iterations.
Little Omega denotes "more than" <expression> iterations.
Understanding Notations of Time Complexity with Example
O(expression) is the set of functions that grow slower than or at the same rate as expression. It indicates the maximum required by an algorithm for all input values. It represents the worst case of an algorithm's time complexity.
Omega(expression) is the set of functions that grow faster than or at the same rate as expression. It indicates the minimum time required by an algorithm for all input values. It represents the best case of an algorithm's time complexity.
Theta(expression) consists of all the functions that lie in both O(expression) and Omega(expression). It indicates the average bound of an algorithm. It represents the average case of an algorithm's time complexity.
The order of growth is how the time of execution depends on the length of the input. In the above example, we can clearly see that the time of execution linearly depends on the length of the array. The order of growth will help us to compute the running time with ease. We will ignore the lower order terms since the lower order terms are relatively insignificant for large input. We use a different notation to describe the limiting behavior of a function.
O-notation: To denote asymptotic upper bound, we use O-notation. For a given function g(n), we denote by O(g(n)) (pronounced “big-oh of g of n”) the set of functions: O(g(n))= { f(n) : there exist positive constants c and n0 such that 0≤f(n)≤c∗g(n) for all n≥n0 }
Ω-notation: To denote asymptotic lower bound, we use Ω-notation. For a given function g(n), we denote by Ω(g(n)) (pronounced “big-omega of g of n”) the set of functions: Ω(g(n))= { f(n) : there exist positive constants c and n0 such that 0≤c∗g(n)≤f(n) for all n≥n0 }
Θ-notation: To denote asymptotic tight bound, we use Θ-notation. For a given function g(n), we denote by Θ(g(n)) (pronounced “big-theta of g of n”) the set of functions: Θ(g(n))= { f(n) : there exist positive constants c1,c2 and n0 such that 0≤c1∗g(n)≤f(n)≤c2∗g(n) for all n>n0 }
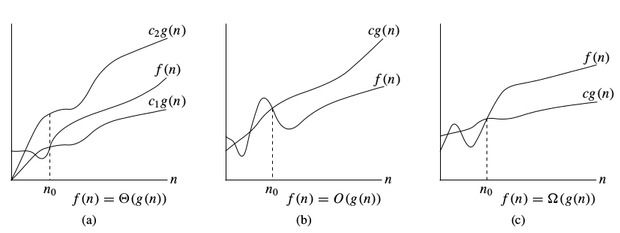
While analyzing an algorithm, we mostly consider O-notation because it will give us an upper limit of the execution time.
Apriori and Apostiari Analysis
Apriori analysis means analysis is performed prior to running it on a specific system. This analysis is a stage where a function is defined using some theoretical model. Hence, we determine the time and space complexity of an algorithm by just looking at the algorithm rather than running it on a particular system with a different memory, processor, and compiler.
Apostiari analysis of an algorithm means we perform an analysis of an algorithm only after running it on a system. It directly depends on the system and changes from system to system.
In industry, we cannot perform Apostiari analysis as the software is generally made for an anonymous user, which runs it on a system different from those present in the industry.
In Apriori, it is the reason that we use asymptotic notations to determine time and space complexity as they change from computer to computer; however, asymptotically they are the same.
MCQ on Complexity Analysis
1. What is the time, space complexity of following code:
int a = 0, b = 0;
for (i = 0; i < N; i++)
{ a = a + rand();
}
for (j = 0; j < M; j++)
{ b = b + rand();
}
Options:
O(N * M) time, O(1) space
O(N + M) time, O(N + M) space
O(N + M) time, O(1) space
O(N * M) time, O(N + M) space
Output:
3. O(N + M) time, O(1) space
Explanation: The first loop is O(N) and the second loop is O(M). Since we don’t know which is bigger, we say this is O(N + M). This can also be written as O(max(N, M)). Since there is no additional space being utilized, the space complexity is constant / O(1)
2. What is the time complexity of following code:
int a = 0;
for (i = 0; i < N; i++)
{
for (j = N; j > i; j--)
{ a = a + i + j;
}
}
Options:
O(N)
O(N*log(N))
O(N * Sqrt(N))
O(N*N)
Output:
4. O(N*N)
Explanation: The above code runs total no of times = N + (N – 1) + (N – 2) + … 1 + 0 = N * (N + 1) / 2 = 1/2 * N^2 + 1/2 * N O(N^2) times.
3. What is the time complexity of following code:
int i, j, k = 0;
for (i = n / 2; i <= n; i++)
{ for (j = 2; j <= n; j = j * 2)
{ k = k + n / 2;
}
}
Options:
O(n)
O(nLogn)
O(n^2)
O(n^2Logn)
Output:
2. O(nLogn)
Explanation:If you notice, j keeps doubling till it is less than or equal to n. Number of times, we can double a number till it is less than n would be log(n). Let’s take the examples here. for n = 16, j = 2, 4, 8, 16 for n = 32, j = 2, 4, 8, 16, 32 So, j would run for O(log n) steps. i runs for n/2 steps. So, total steps = O(n/ 2 * log (n)) = O(n*logn)
4. What does it mean when we say that an algorithm X is asymptotically more efficient than Y? Options:
X will always be a better choice for small inputs
X will always be a better choice for large inputs
Y will always be a better choice for small inputs
X will always be a better choice for all inputs
2. X will always be a better choice for large inputs
Explanation: In asymptotic analysis we consider growth of algorithm in terms of input size. An algorithm X is said to be asymptotically better than Y if X takes smaller time than y for all input sizes n larger than a value n0 where n0 > 0.
5. What is the time complexity of following code:
int a = 0, i = N;
while (i > 0)
{ a += i; i /= 2;
}
Options:
O(N)
O(Sqrt(N))
O(N / 2)
O(log N)
Output:
4. O(log N)
Explanation: We have to find the smallest x such that N / 2^x N x = log(N)

Comments